Quote:
Originariamente inviato da Ziosilvio
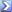
Per dimostrare che una serie di funzioni f_n converge uniformemente ad una somma S in un certo insieme U, devi far vedere che, detta S_n la somma parziale dei termini fino all'n-esimo, comunque preso e > 0, puoi trovare k >= 0 dipendente da e ma non da x, tale che, se n > k, allora |S_n(x) - S(x)| < e per ogni x in U.
Tipico esempio con le serie di potenze:
La serie di funzioni f_n(x) = x^n converge uniformemente nell'intervallo (-1/2, 1/2) alla funzione S(x) = 1 / (1-x).
Questo perché la serie resto è:
-S_n(x)={%5Csum_{k%5Cgt{n}}}{x^k}=x^{n+1}{%5Csum_{k%5Cgeq{0}}}{x^k}=x^{n+1}S(x))
e puoi maggiorare in modulo x^{n+1} con 1/2^{n+1} ed S(x) con 2. |
non so, io continuo a non capire all'atto pratico la convergenza uniforme. concettualmente e graficamente ho capito il significato, ma non riesco ad applicarlo.
per esempio, prendiamo una banale serie di funzioni del tipo: Σ(sin(nx)/n^2);
se non erro converge assolutamente per ogni x, poiché il valore assoluto del seno è sempre minore di 1, e 1/n^2 è serie armonica di secondo ordine e quindi converge;
ora se volessi stabilire se converge totalmente? intanto, con il fatto che ho convergenza su tutto R già mi crea confusione, perché la convergenza uniforme mi pare di averla vista applicata solo su intervalli limitati
devo cercare un massimo della funzione, fissato n, e vedere se converge?