
 |
Quote:
Z{ (k(n) / n!) * a^k * 1(k) } = z / (z - a)^n Con k(n) = k! / n! Quindi per n = 3: f(k) = (k! / 36) * 3^k * 1(k) |
Calcolare a meno di 1/100
 Io per prima cosa mi sono chiesto, ma a +oo diverge o converge? Se diverge non posso calcolare nulla. [ha senso il mio ragionamento fino a questo punto?] Ho sviluppato l'integrale in questo modo:  Primo pezzo: diverge a +oo ~ 1/√t Secondo pezzo: diverge a +oo ma moltiplicato per -1 quindi -oo Terzo pezzo: converge Problema : ho +oo -oo. Si potevo evitare l'integrazione per parti ma speravo che risolvesse il problema +oo -oo. Vedo come si comporta la funzione iniziale confrontandola con 1/√t. Il lim di f(x)\g(x) mi esce 0, quindi g diverge ma g(x)>f(x) quindi non posso dire cosa fa f(x). Non sapendo dimostrare che diverge, prendo per buono che converge a qualcosa e quindi posso calcolare il valore sostituendo qualcosa. Idee? :help: |
Quote:
|
Quote:
prova a vedere questo PDF: http://www.dm.unito.it/quadernididat...statistica.pdf Io e molti altri, si può dire che abbiamo passato statistica grazie a quelle dispense: grande prof la Garetto. |
Quote:
prova a vedere questo PDF: http://www.dm.unito.it/quadernididat...statistica.pdf Io e molti altri, si può dire che abbiamo passato statistica grazie a quelle dispense, per me molto chiare: grandissima la Garetto. ciao |
Conoscete un software sul pc per risolvere un'equazione non esplicitabile?
Ho la Texas ti-89 che è perfetta, ma il calcolo è bello pesante, e ci mette minuti a macinarlo. Ora per esempio ho sbagliato una cavolata e devo aspettare un'eternità :doh: Faccio una cosa del genere: risolvi(f(x)=a,x) Esiste un qualcosa del genere sul pc? che almeno sfruttando la cpu faccio prima :D Non alla matlab insomma, ma più come la Texas detta (se possibile). Una cosa molto semplice. Ho cercato in giro ma non trovo quello che voglio... Grazie ;) |
Quote:
|
Quote:
|
Quote:
Giusto un paio di domande: - come indico la funzione e (inverso del ln)? Se dico "%e^()" come inverso mi da log e non ln. - come farsi restituire il risultato finale a numero? Ovvero risolvendo qualcosa arriva ad x=a+b/log(c) tanto per dire, avendo con abc i numeri e quindi calcolabile. grazie ciao ;) EDIT: ok, log è ln. |
Quote:
Idee su come calcolare il valore dell'integrale a meno di 1/100? Mi hanno suggerito qualche sostituzione del tipo y=100/t o simile, poi provo. |
Quote:
ciao ;) |
Quote:
|
Quote:
|
Su wiki sono riuscito a studiare un po', è fatto meglio di quanto pensassi ;)
Quote:
(il resto mi ha fatto paura... tu a biotech hai studiato tutta sta roba di calcolo? Analisi 1 non lo passerò manco col libro davanti :O ) |
Quote:
Porti 1/sqrt(t) dentro alla sommatoria (costante rispetto alla sommatoria). Ora devi verificare l'assoluta convergenza dell'argomento della sommatoria. Se è verificata (e credo proprio si sì), allora puoi scambiare l'integrale con la serie. Fai l'integrale dell'argomento della serie e poi ti resta da lavorare sulla serie. |
Quote:
|
[Ricerca Operativa]
Ragazzi,
tra qualche giorno dovrò sostenere un esame di ricerca operativa...mi sono un attimino incartato sull'ultimo punto di un esercizio di un vecchio compito. Il testo dice così: Sia dato il seguente PL: max{x1 − x2 : −x1 + x2 ≤ 2; 4*x1 + x2 ≤ 12; x2 ≤ 3; x1 , x2 ≥ 0}. 1) Trovare la soluzione ottima usando il metodo che si ritiene opportuno Vabbè questo è un banale problema di PL in cui ho delle disequazioni anzichè delle equazioni...per risolverlo lo porto in forma standard introducendo delle variabili di slack x3, x4, x5 in modo tale da avere euazioni al posto delle disequazioni. Inoltre cambio la funzione obbiettivo che da max mi diventa min cambiando i segni della funzione obbiettivo. Quindi avrei qualcosa tipo min{-x1 + x2 : −x1 + x2 +x3 = 2; 4*x1 + x2 + x4 = 12; x2 + x5 = 3; x1 , x2 ≥ 0}. A questo punto applico il metodo del simplesso costruendomi il tableau e mi sono trovato che la SOLUZIONE OTTIMA è: x1 = 5 x2 = 2 x5 = 3 e che la funzione obbiettivo vale z = 3 Questa parte dovrebbe essere sicuramente giusta Poi l'esercizio mi chiede: Scrivere il problema duale del PL Ed anche questa cosa è abbastanza semplice, basta applicare le regoline e partendo dal problema di partenza datomi nel testo (quello con la funzione obbiettivo max) mi sono trovato il duale che dovrebbe essere: min{2*u1 + 12*u2+ 3*u3: VARIABILI: u1 >= 2; u2 >= 12; u3 >= 3 VINCOLI: -u1 + 4*u2 <= 2; u1 + u2 + u3 <= -1} Ed anche questo dovrebbe essere corretto... Ora la parte su cui mi blocco e che non ho la minima idea di cosa debba fare è la seguente: Determinare la soluzione ottima del problema duale, utilizzando le condizioni di ortogonalità Sul libro non sono riuscito a trovare nulla e neanche nei miei appunti...da quel poco che mi ricordo delle lezioni mi pare che questa cosa si usi quando ho la soluzione ottima del primale e da quella voglia ricavare la soluzione ottima del duale...almeno così credo... Mi sapete dire cosa devo fare e come risolvere? Grazie mille |
ragazzi vi prego vorrei solo una verifica, ho fatto un esercizio ma non so se è giusto, quindi posto la traccia e la mia soluzione e magari quando avete tempo lo fate e mi dite se esce anche a voi cosi..perchè è la prima tipologia di esercizi che faccio cosi, grazie.
Allora si ha una circonferenza generata dall'intersezione di un piano e di una sfera : x-y=0 (piano) x^2+y^2+z^2-4x-2z=0. Il mio procedimenti è stato il seguente : calcolo centro sfera : (2,0,1). Calcolo raggio sfera : SQRT(5) Per calcolare il centro della circonferenza trovo una retta passante per il centro e ortogonale al piano. PEr essere ortogonale al piano il parametro direttore deve essere uguale ai coefficenti del piano, quindi ho posto l=1,m=-1,n=0. Per scrivere l'equazione parametrica mi avvalgo delf atto che deve passare per il centro qundi x0=2,y0=0,z0=1. Ho trovato cosi la seguente retta parametrica : x=2+t;y=-t;z=1. Porto la retta in cartesiane, svolgo il sistema di interesezione tra retta e piano trovandomi il punto (1,1,1) che dovrebbe essere il centro della circonferenza. Per il raggio della circonferenza trovo inanzitutto la distanza tra piano e centro della sfera, che mi viene SQRT(2). Con la formula r' =r^2 - d(p-C') trovo il raggio della circonferenza, quindi SQRT(5)^2 - SQRT(2)^2 = 5-2 = 3. Quindi la circonferenza ha raggio 3 e centro (1,1,1). Vi trovate? |
ciao ragazzi, una domanda un po' stupida di geometria analitica: alle superiori ci avevano insegnato un metodo per disegnare al volo una qualsiasi retta (y=mx+q) guardando semplicemente m e q. Q è l'intersezione con l'asse y, quindi è immediato.
Col coeff. angolare invece non mi ricordo: in pratica ci spostavamo nel piano cartesiano prima in verticale, poi in orizzontale guardando il valore di m e in qualche modo si otteneva un secondo punto e si poteva tracciare la retta. Non parlo del metodo "per punti", era una cosa molto più immediata... spero di essermi spiegato (e per vostra felicità venerdì ho di nuovo il syllabus e se lo passo vi offro da bere a tutti :sofico: ) |
Bastava guardare su wiki :fagiano:
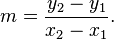 Di due punti A(x1,y1) e B(x2,y2). La lunghezza y e quella x sono date dal numeratore e dal denominatore della formula coefficiente angolare. Ops, ho letto male :asd: Penso che sia così: considera che si tratta sempre di un rapporto. Se hai y=5x+1 il cinque sarebbe un m= 5/1, quindi ottieni lunghezza x=1 e y=5, forse :stordita: |
| Tutti gli orari sono GMT +1. Ora sono le: 13:31. |
Powered by vBulletin® Version 3.6.4
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.
Hardware Upgrade S.r.l.