
 |
Quote:
|
Quote:
|
Quote:
cioè, sempre considerando l'esempio di prima, io avrei scritto che: fino a qua sono giuste le scomposizioni? sperando di sì :stordita: , avrei poi riscritto il limite come:  e adesso non posso applicarela regola che mi hai detto tu qui sopra, no? e quindi non so come andare avanti..scusate se sono domande stupide ma non saprei neanche dove studiare queste cose..ho cercato sul libro, ma liquidano l'argomento troppo velocemente! Grazie |
Quote:
Quote:
|
Quote:
allora Stesso discorso per la tangente. Quote:
Quote:
Adesso rifai le stime... |
Quote:
Quote:
Quote:
|
Quote:
per il primo limite..sarebbe sbagliato se considerassi il limite notevole (tan x - sen x)/x^3 invece che i singoli tan x e sen x? EDIT Ho provato a farlo decomponendo singolarmente senx e tanx e mi viene questo:  (se non ho copiato male..) al numeratore poi posso semplificare le due radici di x e poi mi rimangono i due o(x) e x (che è quello a cui devo arrivare se voglio poi togliere gli o piccoli, no?)..e al denominatore invece come procedo? Grazie |
Quote:
Quote:
Quote:
Ma A è comunque una collezione di... numeri. Uno per ogni intero diverso da 0. Il fatto che tu creda che sia illimitato dipende dall'idea che hai di iperbole, che è corretta ma non corrisponde all'insieme A. Prova a sostituire a k qualche valore e ti accorgerai subito di come vanno le cose... ;) |
Ah, tutto chiaro... io confondevo la retta (R) con il piano (che invece è R^2, perché X x Y = R x R, se non sbaglio), quindi quelli sono solo punti di una retta e, effettivamente, provando si vede subito con k = -1 si ha il minimo, perché con valori di k < -1 la "x" diminuisce sempre di più tendendo a pi greco all'infinito.. grazie sei stato chiarissimo :)
|
Quote:
è l'insieme di tutti gli oggetti che appartengono ad almeno uno degli insiemi X{i}. Discorso simile per l'intersezione. Quote:
I punti di un'iperbole, invece, giacciono su un piano. |
Wow!
Certo che uno non può neppure assentarsi per un solo pomeriggio - pallosissimo collegio docenti in cui si approvano i soliti progetti ben pagati di chi non entra mai in classe per far lezione... :grrr: - che voi ne macinate di roba! All'utente blue_blue dico di non prendersela: alcuni sono proprio fissati col simbolismo di Landau! A Zio Silvio chiedo invece se preferisce che il monumento gli venga eretto in terra italica o d'Islanda. :ciapet: |
scomposizione
salve, volevo sapere un metodo univoco e generale per scomporre un denominatore già sottoforma di prodotto di polinomi. Conosco il metodo specifico per alcuni casi semplicissimi: il metodo dovrebbe essere quello dell'uso di due (nel caso siano due i fattori a denominatore) variabili A e B e la ricongiunzione delle frazioni parametrizzate con al numeratore della prima la costante A e la costante B al secondo numeratore.
avevo avuto una mezza intuizione (probabilmente errata) a riguardo: mi sembra che risultava corretto se in ogni frazione parametrizzata mettevo un polinomio di grado inferiore di 1 rispetto a quello del suo denominatore. Ma non sono ancora arrivato alla conclusione di alcuni esercizi che prevedono questo uso.. aspetto impaziente ciao a tutti! |
Quote:
Mah... se ho ben capito, vuoi scomporre una frazione algebrica nella somma di più frazioni, o sbaglio? E' il metodo di decomposizione delle funzioni razionali fratte, che di solito viene introdotto quando si studiano i metodi di integrazione. In generale, il principio su cui fonda la regola è sempre lo stesso, ma va adattato a seconda della natura delle soluzioni (reali e distinte, coincidenti, complesse distinte, complesse con molteplicità) che presenta il polinomio a denominatore... Trovi i vari casi in un qualunque libro che tratti i metodi di integrazione delle funzioni razionali fratte. |
Quote:
Quote:
Ora seguirà una trattazione di un certo livello, ma che indica un metodo generale come dicevi tu. Se non capisci cosa voglio dire, ed i simbolismi che uso, dimmelo subito! In ogni caso, ti consiglio di dare un'occhiata all'esempio in fondo. In generale, si tratta di trovare dei polinomi q_i(x) tali che dove possiamo scrivere A questo punto, scrivendo Esempio Nell'ultimo esempio che ti ho scritto, si ha m_1 = 4 e m_2 = 2, dunque M = 6 e m = 2, da cui g_1 = 2 e g_2 = 0 (una costante). Quindi le nostre incognite sono i coefficienti b_10, b_11 e b12 di q_1(x), e b20 di q_2(x). Sviluppando al numeratore l'espressione otteniamo il polinomio Ora, come ho detto, i coefficienti dei termini di grado da 1 in su devono essere nulli, mentre il termine noto deve essere pari ad 1. Si tratta quindi di risolvere il sistema Si tratta di un sistema con 5 equazioni (di cui due uguali) e 4 incognite, ma è risolubile: Quindi: |
una domanda abbastanza banale e fine a se stessa... ma pensare
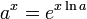 e usare la seconda parte dell'ugualianza è la stessa cosa nell'uso "giornaliero" (nella derivazione è molto comodo)??? e usare la seconda parte dell'ugualianza è la stessa cosa nell'uso "giornaliero" (nella derivazione è molto comodo)??? |
1 Allegato(i)
scusate un attimo
l'equazione che ho messo in allegato, con z complesso e k reale diverso da 0, tralasciando l'argomento che dovrebbe assumere z, ammette soluzioni solo per k=+-1? |
Quote:
;) |
[mate] proiezione vettore su procedimento di Gram-schmidt
Salve a tutti, non riesco a capire perchè nel procedimento di Gram-Schmidt cioè il procedimento con il quale da un sottospazio finitamente generato si riesce a ricavare una base ortonormale di vettori, per trovare la proiezione ortogonale di un vettore si moltiplica per 2 volte per il vettore ortonormale precedente.
Cioè: w2' = v2 - (v2 * w1) * w1 perchè moltilplico 2 volte? la proiezione parallela a w1 non mi è già data moltiplicando una volta solo il vettore per w1? Grazie |
Quote:
La seconda moltiplicazione è un prodotto di uno scalare per un vettore: uno scalare e un vettore in input, un vettore in output. Quote:
Infatti quello che fai è togliere da w2 la componente parallela a w1, lasciando solo quella ortogonale. A questo punto, il sistema {w1,w2'} non può che essere ortogonale. |
Salve ragazzi.
Avrei bisogno di aiuto con queste equazioni differenziali: La prima è facile ma il risultato che vien fuori a me è diverso da quello del mio libro, eccovela: Si legga: [(d^2\dx^2)P]: derivate seconda di P in x quadro. [(d\dx)P]: derivata prima di P in x. D è una costante. E ed u sono delle costanti. D * [(d^2\dx^2)P] = (P-p)\T Le condizioni al contorno sono queste: P( x = 0 ) = P(0) = costante. P(x à inf) = p Ovviamente chiede la soluzione P(x). Poi mi chiede di risolvere la stessa equazione mantenendo invariata la prima condizione al contorno e modificando la seguente come segue: P(W) = p con W un valore di x diverso da infinito ma più grande di 0. In questa viene fuori il seno iperbolico:Buonasera!!! Poi eccovi l’altra equazione: [(d\dt)P] = -uE[(d\dx)P] + [(d^2\dx^2)P] -(P-p)\T Trovare P(x,t) prima per E=0 e poi per E diverso da 0. Chi mi aiuta? Dario |
| Tutti gli orari sono GMT +1. Ora sono le: 19:15. |
Powered by vBulletin® Version 3.6.4
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.
Hardware Upgrade S.r.l.